推荐学习书目
› Learn Python the Hard Way
Python Sites
› PyPI - Python Package Index
› http://diveintopython.org/toc/index.html
› Pocoo
值得关注的项目
› PyPy
› Celery
› Jinja2
› Read the Docs
› gevent
› pyenv
› virtualenv
› Stackless Python
› Beautiful Soup
› 结巴中文分词
› Green Unicorn
› Sentry
› Shovel
› Pyflakes
› pytest
Python 编程
› pep8 Checker
Styles
› PEP 8
› Google Python Style Guide
› Code Style from The Hitchhiker's Guide
这是一个创建于 1754 天前的主题,其中的信息可能已经有所发展或是发生改变。
代码
import numpy as np
a=np.mat([
[538084012500000.0, 6832812857142.857, 88573500000.0, 1180980000.0, 16402500.0, 243000.0, 4050.0, 90.0],
[47829690000000, 531441000000, 5904900000, 65610000, 729000, 8100, 90, 1,],
[13348388671875, 177978515625, 2373046875, 31640625, 421875, 5625, 75, 1,],
[2799360000000, 46656000000, 777600000, 12960000, 216000, 3600, 60, 1,],
[373669453125, 8303765625, 184528125, 4100625, 91125, 2025, 45, 1],
[21870000000, 729000000, 24300000, 810000, 27000, 900, 30,1 ],
[170859375, 11390625, 759375, 50625, 3375, 225, 15, 1],
[0, 0, 0, 0, 0, 0, 0, 1]])
print(np.linalg.det(a))
print(np.linalg.det(a)*np.linalg.det(a.I))
print(a*a.I)
输出
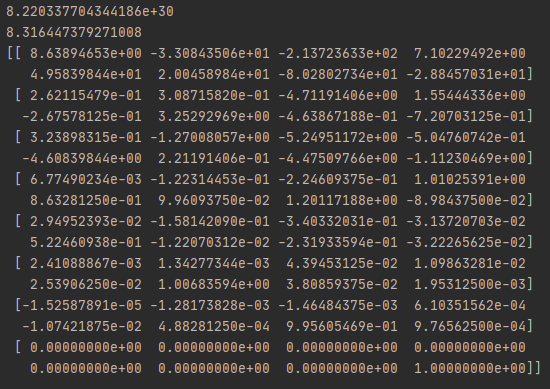
det(a)不等于 0,所以 a 应该是可逆的
但是 det(a)*det(a.I)不等于 1,
a*a.I 也不是单位矩阵
1
shenyi97 2021-01-08 20:30:58 +08:00
矩阵的数字太大,精度不够,同样的过程在小矩阵上是没问题的。
|
2
jc89898 2021-01-08 20:36:06 +08:00
你还是回去多学习学习吧,很多操作都是 numeric approx,肯定不可能完全是 identity 。
|
3
nightwitch 2021-01-08 21:57:30 +08:00
数值不稳定呗,数值分析里常讨论的问题
|
4
CrazyRundong 2021-01-08 22:51:02 +08:00 via iPhone
数值方法的稳定性问题。求逆时对矩阵会做 LU 分解,再加上矩阵的存储和计算都是 float,会有额外的数值误差
https://mathworld.wolfram.com/MatrixInverse.html |
5
Ayahuasec 2021-01-09 13:00:16 +08:00
感觉参考一下摄动定理。
矩阵的单个或多个元的误差会导致求逆的结果出现较大的差别。 计算机存浮点的时候是有精度的,参与计算的时候相当于会引入误差。 取一个极端一点的例子,比如 A=[2,6;2,6.1];B=[2,6;2,5.9]; 就一个元差了 0.2,但是 inv(A)=[30.5,-30;-10,10];inv(B)=[ -29.5000,30.0000;10.0000,-10.0000]; 求完逆都接近 inv(A)==-inv(B)了。 |
6
necomancer 2021-01-10 01:37:32 +08:00
没看出这和摄动定理有啥关系,感觉只是数字太大的精度问题,原则上应该是
if np.linalg.cond(a) < 1/sys.float_info.epsilon: ....ainv = np.linalg.inv(a) else: .... 你的体系 condition 已经是 1e26 了,float 没法做好的。 condition 巨大目前没有什么好办法,而我大概试了一下,好像转换成 np.longdouble 也不行……然后用 np.finfo 看了一下,好像 np.float 默认是 np.longdouble, np.longfloat.... 建议方案: -2. 如果是厄密矩阵,可以考虑 scipy.sparse.linalg.cg ,emm……最优先建议你重新考虑一下你的问题,重新设计解决方案和找观察量。而且矩阵元差这么大是所有矩阵元都是幂指数的形式么?看看有没有相关的数学性质能简化问题? -1. 用 preconditioner 然后求解 Ax=I,一般试试 Jacobi preconditioner,我试了,你这个体系好像不太行……SOR 一类的我没试,不知道基于迭代的话效果会不会好一些 0. 试试 moore-penrose pseudoinverse 低精度先试试这个,说不定就好用了,比如你例子里如果 np.linalg.pinv(a, rcond=1e-20).dot(a) 看着效果还行~至少比你给的要好 1. 用别的库,支持更长的 double 的库,可以试试 mpmath,一个 python 库,据说只是速度略拉跨 2. 即便用了高精度的库,遇到大 condition 体系,一般来说也别直接就求逆,试试用 svd 求 u,s,vT,然后 a^-1=vs^{-1}uT,例如 u,s,vt=np.linalg.svd(a) np.dot(vt.transpose(),np.dot(np.diag(s**-1),u.transpose())) |
7
necomancer 2021-01-10 02:36:19 +08:00
In [23]: from mpmath import *
In [24]: mp.dps = 100; mp.pretty = True In [25]: m Out[25]: [538084012500000.0 6832812857142.857421875 88573500000.0 1180980000.0 16402500.0 243000.0 4050.0 90.0] [ 47829690000000.0 531441000000.0 5904900000.0 65610000.0 729000.0 8100.0 90.0 1.0] [ 13348388671875.0 177978515625.0 2373046875.0 31640625.0 421875.0 5625.0 75.0 1.0] [ 2799360000000.0 46656000000.0 777600000.0 12960000.0 216000.0 3600.0 60.0 1.0] [ 373669453125.0 8303765625.0 184528125.0 4100625.0 91125.0 2025.0 45.0 1.0] [ 21870000000.0 729000000.0 24300000.0 810000.0 27000.0 900.0 30.0 1.0] [ 170859375.0 11390625.0 759375.0 50625.0 3375.0 225.0 15.0 1.0] [ 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0] In [26]: n = m ** -1 In [27]: nprint(n*m) [ 1.0 2.04417e-89 2.61884e-91 3.42987e-93 4.52015e-95 6.19423e-97 9.03116e-99 1.93102e-100] [-2.40032e-85 1.0 -3.91747e-89 -5.15496e-91 -6.69831e-93 -9.01131e-95 -1.22414e-96 -2.51457e-98] [ 1.76004e-83 2.24203e-85 1.0 3.76075e-89 4.80636e-91 6.37293e-93 8.01006e-95 1.5947e-96] [-6.48049e-82 -8.1386e-84 -1.01194e-85 1.0 -1.6932e-89 -2.26687e-91 -2.73878e-93 -6.08618e-95] [ 1.11031e-80 1.39958e-82 1.72213e-84 2.41363e-86 1.0 4.24722e-90 4.96632e-92 1.30338e-93] [ -7.611e-80 -9.60395e-82 -1.13408e-83 -1.80567e-85 -2.19884e-87 1.0 -3.55957e-91 -1.3663e-92] [ 3.23187e-79 3.7357e-81 3.70454e-83 6.05774e-85 5.43644e-87 7.24858e-89 1.0 1.53409e-92] [ 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0] In [28]: |