这是一个创建于 1246 天前的主题,其中的信息可能已经有所发展或是发生改变。
Linear Algebra In Diagrams 是什么?
Linear Algebra In Diagrams 是我学习线性代数时整理的一份笔记,它基于 Brown University 的 Linear Algebra Done Wrongs by Sergei Trei 。
和大部分“字典式的“笔记不同的是,它包含了大部分重要的证明、定理以及(最重要的)一些插图,并按照我认为最合理的叙事逻辑来讲述。我相信这样的写作形式能让它变得更加易读。而我想它也一定程度做到了——在四个月里,我经常因为其他事由间隔两三周再继续学习和创作;而它也几次帮助我快速拾起一些几乎遗忘的知识和技巧。
和书本不同的是,我尽量保持了它的简短性。同时,我也尝试回答了书本中不会明说的一些“为什么”:比如一些证明中使用的量为什么这么构造,为什么 Einstein notation 的 rules 这么规定。当然最重要的是它包含了许多插图,这些插图总结了一些重要概念的关系、证明的步骤,能让我快速回忆或记忆相关内容。
当然缺点也比较直接:为了避免赘述,我只包含了我想 comment 或补充的主题,省略了如 determinant 等主题。所以它可能不适合作为书本的直接替代。但是我希望它能减轻学习成本。
特点
-
尽可能通过图像具象化了定理的证明和结论,并总结章节内容,更好地来建立对它们的直觉。
-
连贯且精炼的介绍了从线性空间到张量初步的几乎所有内容。
-
尝试对概念、符号、定理构造的动机进行解释
适合:
-
作为初学线性代数时的补充
-
对基础定理的证明作快速复习
-
想提升对一些基础定理的直觉理解
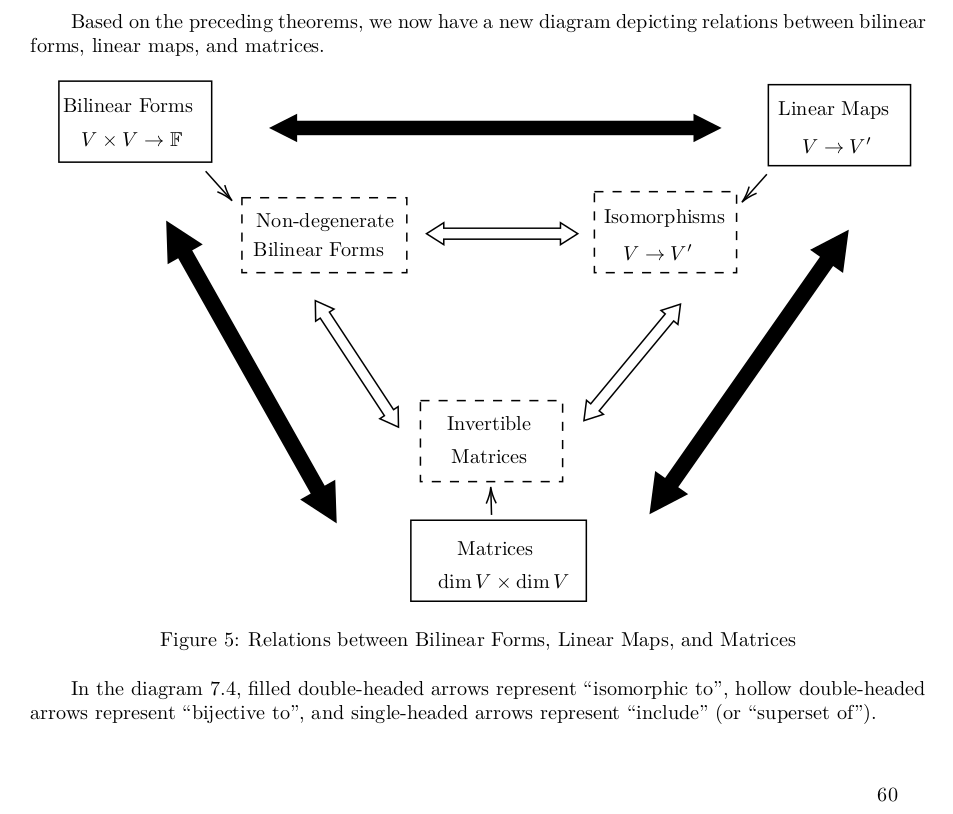
一些截图

如何阅读
笔记发布在FLibrary上,可以在笔记页面免费获取最新 PDF 版本。
笔记目前处于初稿阶段,可能存在 typo 等错误。如有疑问或想法可以联系作者(harryying at flibrary.info),非常感谢
1
zhs227 2022 年 9 月 14 日
网站有点难用,用三方帐号登录以后很长时间(约 10 分钟)刷新笔记页面仍然提示“Sign in to ...”,后面好不容易找到了,也 purchase 成功以后,刷新笔记页面仍然提示 purchase ,就是看不见下载,虽然下载了我也可能看不懂,但是体验不好。
|
2
LEXUGE OP |
3
WillBC 2022 年 9 月 14 日
|
4
LEXUGE OP @WillBC 很不错的资料!
我粗略看了一下,它的 interactive parts 应该是注重于 example,可以直观看到结果. LAID 的插图比较 generalized, 笔记里也比较少有 examples. 后续或许会增加 |
5
ColorfulBoar 2022 年 9 月 14 日
这网站设计得好抽象,卡到一度怀疑是我浏览器在整蛊
假如你真的是照着那个学的那难怪那书叫 done wrong ,看起来是不太对劲,done right 不都示范了怎么做了吗,咋还念念不忘 matrix…… 这个领域正经的 diagram 就一种:string diagram (广义的,包括各种乱七八糟的变种,其中交换图和 Penrose diagram 是比较出名的两种),这个越多越好,剩下的图都没用,画得越多距离形成正确的直觉就越远。扫了一眼幸好(虽然标题那么写了但)一共也没几张图 最后那章 tensor 问题比前面更大(哪怕写了好几页才讲了个定义)。那个求和约定其实是抽象指标,实际上是先有一个描述了 tensor 怎么缩并的图,然后大家懒得画图就把图上的线用字母代替了,这个字母就是所谓的抽象指标,上下标其实是线的两端。它发明出来是用来坐标无关地做计算的,你完全理解反了,所以最后才发明出来一个纯添乱的新记号…… |
6
LEXUGE OP @ColorfulBoar 感谢你的批评!
网站是纯 HTML 的,可能在反应上并不是很友好。 Done Right 我其实也看了。能具体说一下哪里“念念不忘 matrix”吗? 谢谢你的指点,我一直想找一些 category theory 的 diagrams 来入门,因为没有找到好的材料,就直接用了一些原始的方法来作图。 最后,tensor 入门在我看的其他几本书中都未涉及( Linear Algebra by Serge Lang, "Done Right"),所以只是最简单的从 basis 出发做了一些介绍。请问你有什么 tensor 和 penrose diagram 的 reference (书本、文章、笔记等)可以推荐吗?感激不尽。 |
7
ColorfulBoar 2022 年 9 月 15 日
@LEXUGE #6 那两个对比一下很明显,done right 对 matrix 的引入是能拖就拖,所以里面绝大多数证明都是坐标无关的,反过来你这个里面太多没必要的分量下的计算了,反而模糊了重要的结构
category of vector spaces (作为 abelian category )性质太特殊了所以你才找不到合适的材料,这个阶段这么做没什么意义,能理解的例子太少了。其实「直觉」不一定是几何直觉,我感觉对于线性代数来自量子力学的直觉更有效 tensor 有很多种画风,如果你一定要跟线性代数混在一起的话那某本苏联人写的书是这样的(但我并不推荐它……)。正经讲抽象指标的只有 Penrose 自己的书( spinors and spacetime 前两章和附录),剩下的基本上都是在随便忽悠一下 |
8
hackpro 2022 年 9 月 15 日 via iPhone
@ColorfulBoar #7 我也觉得直觉 intuition 很重要啊 但是引入量子力学的话大部分读者都不一定具备这个基础 所以还是用通用的例子比较好
|