V2EX › 推广
机器学习&量化投资-从入门到放弃全套笔记-Logistic Regression (上)
datayes2015 · 2016-12-09 13:13:33 +08:00 · 6970 次点击这是一个创建于 3239 天前的主题,其中的信息可能已经有所发展或是发生改变。
1 、首先明确学习 机器学习 的动机
先放一张大神的照片

不知道他的同学,点这里: http://baike.baidu.com/link?url=f7gg3CfSgV0FnVShzVofMK65MC3UU6kfUbK0_RupJ0ZHr4rG2UCfYWz5PEHjxqodrhf0O22RKKXJhi3NiCVZxa
詹姆斯·西蒙斯在 TED 的对话中有提到:
Q :机器学习在这里扮演了怎样一个角色?
A :某种意义上,我们做的就是机器学习。你观察一大堆数据,模拟不同的预测方案,
直到你越来越擅长于此。我们所做之事,不见得一定有自我反馈,但确实有效。
视频地址: https://v.qq.com/x/page/s0186b0yrpw.html
然而现在有许多已实现的机器学习开源包可供我们调用,如 sklearn ,更高级的技术还有 Hadoop 、 Spark 等等。
那么是不是我们只须知道如何将训练数据与测试数据输入到模型,然后调用分类或回归的结果就好了呢?
理解其数学原理,自己再实现一遍算法有无必要呢?
在汲取一些前辈的建议以及结合自己的思考后,我觉得自己亲手推一遍数学公式,再用 Python 实现算法还是有必要的。
—因为这样不仅能使我们加深对机器学习本质的理解,还能让我们对模型与数据之间联系更加敏感。
例如,如何选择模型、如何选择特征、如何调整参数等等。
—其次,目前开源的机器学习算法包提供的都是通用型的算法,并非针对量化投资这一领域来进行优化。
所以,当有必要时,我们须根据自己的需求来优化这些通用算法,甚至重写。另一方面,真正有用的算法在量
化领域是不会开源的。
当然机器学习这么多的算法也没有必要全都实现一遍,但常见的算法的核心部分还是要亲手实现的。
2 、本帖的意义
贴主目前只是一个半路入量化坑的在校学生,本身并非研究机器学习这一方向,也不是 CS 科班出生。
但凭借着内心的兴趣还是想扎扎实实地学习机器学习与量化投资的知识,并且希望将来能将两者结合起来做出一些有效的模型或策略。
本贴是一名普通工科生的自学笔记,笔记详细记录了 Logistic Regression 的数学原理与推导过程。在核心公式推导过程中,都会引出并详细解释关键的求解技巧和对应的数学知识。因此,只要是对本科高数还有记忆的同学都能完全理解和掌握。
由于贴主才疏学浅,数学、编程、金融样样不通,本帖中错误与不严谨之处在所难免,希望各位朋友批评指正。
最后,本贴剩余部分结构如下:
3. 介绍 Logistic Regression 的数学模型,推导并详细解释求解最优回归系数的过程;
4. Python 实现 Logistic Regression 的基本版;
5. 介绍 sklearn 中的 Logistic Regression 算法及其关键参数;
6. 实现一个基于 Logistic Regression 的简单选股策略。
今天我将向大家介绍 Logistic Regression 的数学模型,也就是 3.,再下篇帖子中,我将继续介绍 4. 5. 6.,敬请期待。
3 、什么是 Logistic Regression
首先,我们知道机器学习是一系列对数据执行分类、回归和聚类等操作的统计算法的统称,这些算法根据历史数据(训练数据)的特征,来对未来数据(测试数据)进行判断。
本贴我们学习一种最常用也最重要的分类算法— Logistic Regression 。
首先我们引入对数几率函数( logistic function )如下所示:
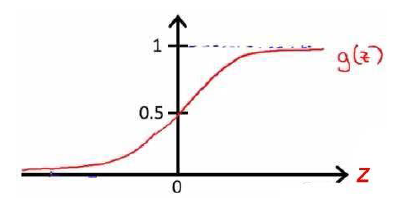
从上图我们可以看出,此函数可将定义域为(-∞, +∞)自变量 z 映射到(0,1)区间。若以 y=0.5 为阈值,我们可以利用这个函数实现一个二分类器:
当 z>0 ( y>0.5),将其划分为 1 类;
当 z<0 ( y<0.5),将其划分为 0 类。
由于于输出 y 为 0 到 1 之间的连续值,我们也可以认为函数是对类别的概率估计。
3.1 若有多个输入变量呢?
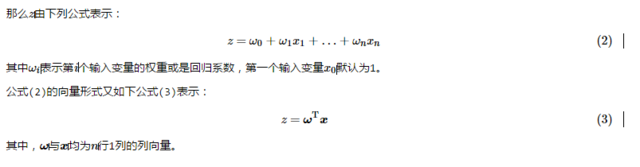
3.2 为什么称有如此形式的函数为对数几率函数呢?

3.3 如何求解回归模型中的最优回归系数(权重)呢?
首先根据公式( 4 )我们可得:
lnp(y=1|x)p(y=0|x)=ωTx(5)
进一步我们不难得到在输入为 x 的情况下,输出类别 y 分别为 1 和 0 的概率为:
p(y=1|x)=eωTx1+eωTx=11+e−ωTx(6.1)
p(y=0|x)=11+eωTx(6.2)
3.3.1 极大似然估计 是求解最优系数的常用方法之一。

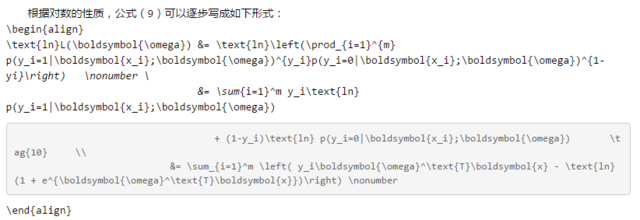
3.3.2 如何求解最优的回归系数 ω 呢?




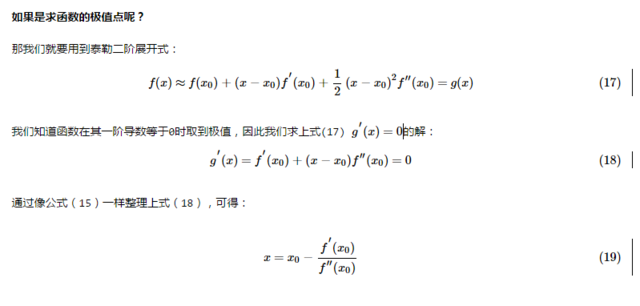

梯度上升法与牛顿法的比较:
梯度法是一阶收敛的,而牛顿法是二阶收敛的。因此牛顿法的迭代次数要少于梯度法,然而 Hessian 的逆矩阵的计算会增加算法的复杂度。
这个问题又可以通过 Quasi-Newton 方法解决,本帖对此方法也不做深入讨论。
敬请期待下篇。
先放一张大神的照片

不知道他的同学,点这里: http://baike.baidu.com/link?url=f7gg3CfSgV0FnVShzVofMK65MC3UU6kfUbK0_RupJ0ZHr4rG2UCfYWz5PEHjxqodrhf0O22RKKXJhi3NiCVZxa
詹姆斯·西蒙斯在 TED 的对话中有提到:
Q :机器学习在这里扮演了怎样一个角色?
A :某种意义上,我们做的就是机器学习。你观察一大堆数据,模拟不同的预测方案,
直到你越来越擅长于此。我们所做之事,不见得一定有自我反馈,但确实有效。
视频地址: https://v.qq.com/x/page/s0186b0yrpw.html
然而现在有许多已实现的机器学习开源包可供我们调用,如 sklearn ,更高级的技术还有 Hadoop 、 Spark 等等。
那么是不是我们只须知道如何将训练数据与测试数据输入到模型,然后调用分类或回归的结果就好了呢?
理解其数学原理,自己再实现一遍算法有无必要呢?
在汲取一些前辈的建议以及结合自己的思考后,我觉得自己亲手推一遍数学公式,再用 Python 实现算法还是有必要的。
—因为这样不仅能使我们加深对机器学习本质的理解,还能让我们对模型与数据之间联系更加敏感。
例如,如何选择模型、如何选择特征、如何调整参数等等。
—其次,目前开源的机器学习算法包提供的都是通用型的算法,并非针对量化投资这一领域来进行优化。
所以,当有必要时,我们须根据自己的需求来优化这些通用算法,甚至重写。另一方面,真正有用的算法在量
化领域是不会开源的。
当然机器学习这么多的算法也没有必要全都实现一遍,但常见的算法的核心部分还是要亲手实现的。
2 、本帖的意义
贴主目前只是一个半路入量化坑的在校学生,本身并非研究机器学习这一方向,也不是 CS 科班出生。
但凭借着内心的兴趣还是想扎扎实实地学习机器学习与量化投资的知识,并且希望将来能将两者结合起来做出一些有效的模型或策略。
本贴是一名普通工科生的自学笔记,笔记详细记录了 Logistic Regression 的数学原理与推导过程。在核心公式推导过程中,都会引出并详细解释关键的求解技巧和对应的数学知识。因此,只要是对本科高数还有记忆的同学都能完全理解和掌握。
由于贴主才疏学浅,数学、编程、金融样样不通,本帖中错误与不严谨之处在所难免,希望各位朋友批评指正。
最后,本贴剩余部分结构如下:
3. 介绍 Logistic Regression 的数学模型,推导并详细解释求解最优回归系数的过程;
4. Python 实现 Logistic Regression 的基本版;
5. 介绍 sklearn 中的 Logistic Regression 算法及其关键参数;
6. 实现一个基于 Logistic Regression 的简单选股策略。
今天我将向大家介绍 Logistic Regression 的数学模型,也就是 3.,再下篇帖子中,我将继续介绍 4. 5. 6.,敬请期待。
3 、什么是 Logistic Regression
首先,我们知道机器学习是一系列对数据执行分类、回归和聚类等操作的统计算法的统称,这些算法根据历史数据(训练数据)的特征,来对未来数据(测试数据)进行判断。
本贴我们学习一种最常用也最重要的分类算法— Logistic Regression 。
首先我们引入对数几率函数( logistic function )如下所示:

从上图我们可以看出,此函数可将定义域为(-∞, +∞)自变量 z 映射到(0,1)区间。若以 y=0.5 为阈值,我们可以利用这个函数实现一个二分类器:
当 z>0 ( y>0.5),将其划分为 1 类;
当 z<0 ( y<0.5),将其划分为 0 类。
由于于输出 y 为 0 到 1 之间的连续值,我们也可以认为函数是对类别的概率估计。
3.1 若有多个输入变量呢?
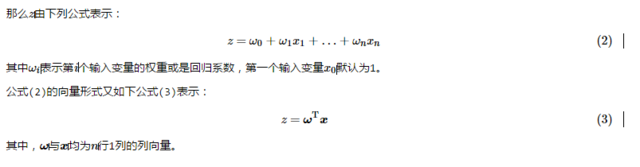
3.2 为什么称有如此形式的函数为对数几率函数呢?

3.3 如何求解回归模型中的最优回归系数(权重)呢?
首先根据公式( 4 )我们可得:
lnp(y=1|x)p(y=0|x)=ωTx(5)
进一步我们不难得到在输入为 x 的情况下,输出类别 y 分别为 1 和 0 的概率为:
p(y=1|x)=eωTx1+eωTx=11+e−ωTx(6.1)
p(y=0|x)=11+eωTx(6.2)
3.3.1 极大似然估计 是求解最优系数的常用方法之一。


3.3.2 如何求解最优的回归系数 ω 呢?




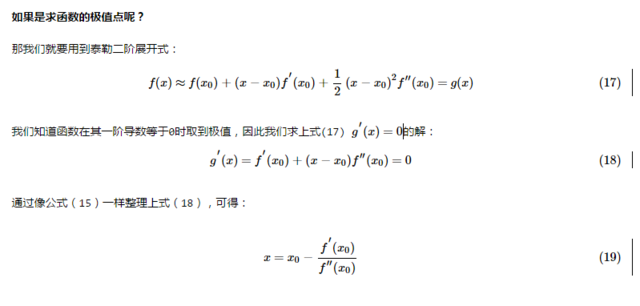

梯度上升法与牛顿法的比较:
梯度法是一阶收敛的,而牛顿法是二阶收敛的。因此牛顿法的迭代次数要少于梯度法,然而 Hessian 的逆矩阵的计算会增加算法的复杂度。
这个问题又可以通过 Quasi-Newton 方法解决,本帖对此方法也不做深入讨论。
敬请期待下篇。
6 条回复 • 2017-11-15 21:50:21 +08:00
1
goodniuniu 2016-12-09 13:45:22 +08:00
等下集!
|
2
datayes2015 OP @goodniuniu 好嘞~感谢您的关注。
|
3
walkingway 2016-12-09 14:10:21 +08:00
排版有些乱,图片不大清晰,能贴一份 MD 版本就好了
|
4
spice630 2016-12-09 14:15:27 +08:00 看来楼主没赚到钱
|
6
wizardforcel 2017-11-15 21:50:21 +08:00
可以顺便把多层 logistic 也补上 =-=
|